异常检测(Anomaly detection)问题: 给定数据集 $x^{(1)},x^{(2)},..,x^{(m)}$,我们假使数据集是正常的,我们希望知道新的数据 $x_{test}$ 是不是异常的,即这个测试数据不属于该组数据的几率如何。我们所构建的模型应该能根据该测试数据的位置告诉我们其属于一组数据的可能性 $p(x)$。
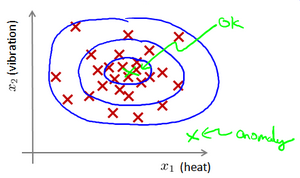
上图中,在蓝色圈内的数据属于该组数据的可能性较高,而越是偏远的数据,其属于该组数据的可能性就越低,这种方法称为密度估计。
欺诈检测:$x^{(i)} = {用户的第i个活动特征}$,模型$p(x)$ 为其属于一组数据的可能性,通过$p(x) < \varepsilon$ (阀值)检测非正常用户。
异常检测主要用来识别欺骗。例如在线采集而来的有关用户的数据,一个特征向量中可能会包含如:用户多久登录一次,访问过的页面,在论坛发布的帖子数量,甚至是打字速度等。尝试根据这些特征构建一个模型,可以用这个模型来识别那些不符合该模式的用户。再一个例子是检测一个数据中心,特征可能包含:内存使用情况,被访问的磁盘数量,CPU的负载,网络的通信量等。根据这些特征可以构建一个模型,用来判断某些计算机是不是有可能出错了。
高斯分布
高斯分布,也称为正态分布。
通常如果我们认为变量 $x$ 符合高斯分布则写做: $x \sim N(\mu, \sigma^2)$,其概率密度函数为: $p(x,\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$
我们可以利用已有的数据来预测总体中的$μ$和$σ^2$的计算方法如下: $\mu=\frac{1}{m}\sum\limits_{i=1}^{m}x^{(i)}$,$\sigma^2=\frac{1}{m}\sum\limits_{i=1}^{m}(x^{(i)}-\mu)^2$
高斯分布样例: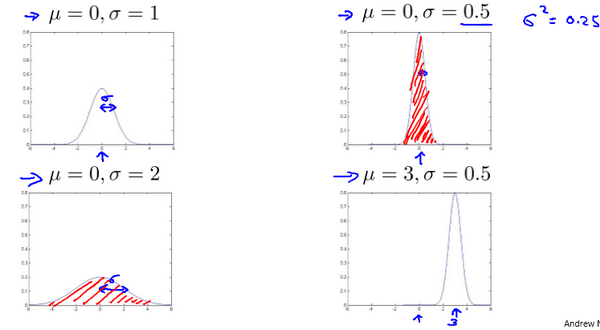
PS: 机器学习中对于方差我们通常只除以$m$而非统计学中的$(m-1)$。这里顺便提一下,在实际使用中,到底是选择使用$1/m$还是$1/(m-1)$其实区别很小,只要你有一个还算大的训练集,在机器学习领域大部分人更习惯使用$1/m$这个版本的公式。这两个版本的公式在理论特性和数学特性上稍有不同,但是在实际使用中,他们的区别甚小,几乎可以忽略不计。